Metody snižování podnikatelského rizika: Prognózování



Prognostické metody mají ve firemních procesech snižování rizika nezastupitelné místo, proto je jim věnována značná pozornost. Řada dále uvedených prognostických metod patří do skupiny metod deterministických, které lze použít při snižování rizika rozhodovacích problémů na operativní nebo na střední úrovni řízení. Poněvadž však dílčím cílem této kapitoly je též prezentace expertního systému pro volbu vhodné prognostické metody, jehož báze znalostí zahrnuje i deterministické modely, budou zde probrány i tyto klasické metody.

Snižovat riziko na únosnou míru ve firmě znamená předvídat, prognózovat a vytvářet varianty možných scénářů vývoje firmy a jejich charakteristik (například zisku, nákladů atd.). Mnoho manažerských problémů vzniká v důsledku neznalosti budoucí situace či neznalosti stupně její neurčitosti. Není proto překvapením, že manažeři věnují značnou pozornost metodám, umožňujícím předpovídat budoucí hodnoty řady proměnných, které ovlivňují jejich rozhodování. V této kapitole se budeme věnovat některým principům předpovídání, respektive prognózování, a předvedeme si některé běžné prognostické techniky. Sledované ekonomické (obchodní) proměnné často vykazují vývojové trendy, které jsou předvídatelné. Poznání a kvantifikování vývojových trendů umožňuje manažerům spolehlivěji a efektivněji rozhodovat. Potřeba prognózování má logické zdůvodnění.

 Rostoucí složitost prostředí, ve kterém musí organizace fungovat a prosperovat, vyvolává spolu s měnícími se požadavky zákazníků potřebu vědět, jak se budou vyvíjet klíčové proměnné, na nichž závisí strategie rozvoje a efektivnosti podnikání.

 Prognóza není v literatuře jednoznačně definována; za společný znak všech definic však lze považovat fakt, že prognóza není jakákoliv předpověď budoucího vývoje, nýbrž předpověď, k níž je přiřazena pravděpodobnost jejího uskutečnění.

Sestavení prognózy je zpravidla pracný a náročný proces, pro nějž nelze poskytnout jednoznačný a přesný návod. Smyslem prognózování je především snížení neurčitosti znalostí o budoucnu.

Manažeři jsou přesvědčeni o tom, že používání prognostických metod a technik jim poskytne dodatečné informace, které jim umožní posoudit alternativní možnosti v kontextu s budoucími podmínkami a vyhodnotit budoucí důsledky současných rozhodnutí. Jaké budou důsledky toho, nezmění-li firma svou dosavadní cenovou politiku? Jak se odrazila změna nákladů o pět nebo deset procent v odbytu konkrétního produktu firmy? Můžeme generovat celou řadu otázek, které mohou manažerovi firmy pomoci při rozhodování.

V procesu analýzy vnějšího i vnitřního prostředí firmy umožňuje prognóza lépe identifikovat příležitosti a hrozby, které na firmu působí. Prognóza vývoje prostředí, v němž firma existuje, má při formování strategie firmy a následně i při formování strategických cílů a hierarchie cílů podnikání velký význam. Dobře zpracovaná prognóza vývoje vnějšího a vnitřního prostředí firmy snižuje riziko a snižuje pravděpodobnost neúspěchu v provádění nutných změn ve firmě.

Je důležité si uvědomit význam prognózování v souvislosti s rozhodovacím procesem, jak je naznačeno na obrázku 5.8.

V centru tohoto procesu najdeme rozhodnutí, která musí manažer uskutečňovat. Tato rozhodnutí jsou bezprostředně ovlivňována zvolenou strategií organizace, zaměřenou na dosažení vytčených cílů a s ohledem na její celkové zaměření a priority. Na rozhodnutí mají značný vliv i informace získané pomocí prognostických metod. Tyto metody poskytující informace o budoucích situacích jsou pro manažery nepostradatelné a spolu s dalšími faktory významně ovlivňují jejich rozhodování. Řada prognózovaných informací ovlivňuje i samotnou tvorbu strategie organizace. Organizace však také potřebuje mít k dispozici účinný monitorovací systém, umožňující sledovat skutečný průběh realizace rozhodnutí a porovnat ho s průběhem plánovaným. V případě zjištění odchylek mezi plánovaným a skutečným průběhem realizace rozhodnutí je třeba použít zpětnou informaci pro korigování prognostického postupu. Bez ohledu na to, zda jsou to odchylky malé či velké, bez ohledu na to, co je jejich příčinou, je třeba stanovit nové předpovědi a celý cyklus začít znovu. Jak uvidíte později, neexistuje ideální prognostický přístup, použitelný pro jakoukoli organizaci. Pro prognózování lze použít řadu alternativních metod a záleží na manažerovi, kterou pro daný rozhodovací problém zvolí.

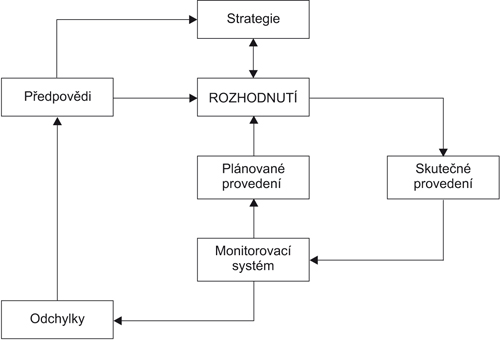
Obr. 5.8 Prognózování a rozhodování

Na obrázku 5.9 jsou zobrazeny přístupy, které jsou v prognostické praxi používány nejčastěji. Zásadně lze tyto přístupy rozdělovat podle toho, zda jsou převážně kvalitativníči kvantitativní. Toto rozdělení může být v některých případech zavádějící, protože některé kvalitativní přístupy produkují numerické výsledky, na druhé straně některé kvantitativní přístupy vycházejí ze subjektivních, kvalitativních předpokladů.

Převzato z knihy Řízení rizik ve firmách a jiných organizacích vydané nakladatelstvím Grada v roce 2013