Metody snižování podnikatelského rizika: Prognózování



Volba vhodné prognostické metody

Tu ovlivňuje především stanovisko manažera k uvedeným předchozím problémům. Volba prognostických technik značně závisí na okolnostech, které se daného prognostického problému dotýkají. Potřebuje-li například velká organizace pro potřeby řízení skladových zásob zpracovávat denní prognózy poptávky pro veškeré skladované položky, je třeba, aby byl prognostický model jednoduchý a aby nevyžadoval neúměrné množství vstupních údajů (použijeme například vyrovnání časové řady pomocí přímky či pomocí polynomu n-tého stupně). Jestliže však stejná organizace potřebuje pro plánování rozvoje svých klíčových výrobků znát dlouhodobou prognózu vývoje poptávky (na dva až tři roky dopředu), bylo by použití jednoduchého exponenciálního vyhlazování neadekvátní.

Podle způsobu, jakým trend (časové řady sledované ekonomické charakteristiky) vyrovnáváme, hovoříme o:

• přímkové (lineární) extrapolaci: f(t) = a₁t + a₀
• kvadratické aproximaci: f(t) = a₂t² + a₁t + a₀
• extrapolaci obecnější – polynomem k-tého stupně: f(t) = a_kt^k + a_k-1t^k–1 + … + a₁t + a₀
• extrapolaci pomocí jiných křivek: exponenciálou nebo logistickou funkcí

Ve výše uvedených vztazích jsou a₀, a₁…reálné konstanty, podobně jako parametry s, a, b.Stupeň polynomu k je přirozené číslo. Tato logistická funkce^[1]se s úspěchem používá zejména při prognózování poptávky po předmětech dlouhodobé spotřeby a při modelování prodeje některých druhů výrobků. Podle typického průběhu se této skupině funkcí též říká tzv. S-křivky.

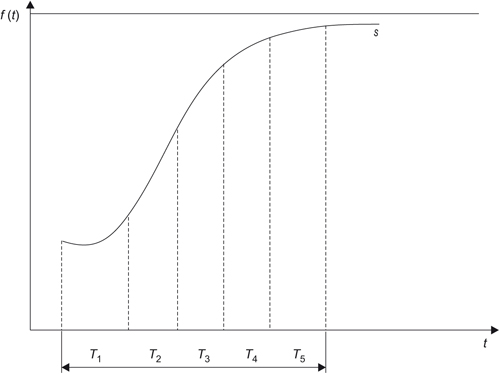
Obr. 5.11 Časové vyjádření vlivu sil, které působí pro změnu a proti ní

Každá S-křivka vymezuje na časové ose pět základních fází působení sil pro změnu a proti ní (například uvedení nového výrobku na trh – konkrétně touto křivkou můžeme modelovat prodej barevných televizorů).

V časovém intervalu T₁se začínají formovat síly, které působí pro změnu (zahájení výroby a prodeje barevných televizorů). Jejich prosazení však brzdí staré síly (působící proti změně), které nejsou zcela překonány (například konzervativní povahou spotřebitele, cenou nového výrobku atd.).

V druhém časovém období se síly, působící pro změnu, začínají plně prosazovat a rozhodující měrou ovlivňují další vývoj. Tyto síly působí jako akcelerátory a tempo vývoje se značně urychluje.

Časový interval T₃je charakterizován situací, kdy změna plně probíhá, formují se však opoziční síly.

V časovém intervalu T₄síly, které působí proti původní změně, nabývají postupně převahu nad silami, které pozbyly svoji progresivnost, čímž se vývojové tendence podstatně zpomalují (například se na trhu objevuje konkurence s technologicky lepším televizorem).

V posledním intervalu T₅ opoziční síly získaly rozhodující převahu a zcela utlumily vývoj dosavadních sil. V této fázi se vývoj zpomaluje až zastavuje, a to do doby působení nových sil, které podpoří (kvalitativně jinou) změnu (například zavedení nového televizoru s novou technologií přenosu obrazu).

Do skupiny S-křivek patří též často používaná Gompertzova křivka, která je tvaru:

• kde koeficient s udává mez saturace (například horní mez prodeje konkrétního výrobku). Při výpočtu parametrů b, cje nejvhodnější logaritmovat původní rovnici Gompertzovy křivky a využít tzv. Kingovy metody.^[2]Mezi klady Gompertzovy křivky patří její značná adaptační schopnost; stanovením různých hodnot parametrů s, b, clze přizpůsobovat Gompertzovu křivku daným časovým řadám.

Pro stanovení konstant a₀, a₁… a_k polynomu k-tého stupně dnes existuje řada metod. Výpočet konstant polynomu se realizuje na počítači, lze proto použít nejpřesnější (i když při „ručním“ výpočtu nejpracnější) metodu – metodu nejmenších čtverců. Pro ilustraci, jak lze uvedeného programu využít pro stanovení koeficientů aproximačního polynomu k-tého stupně, uvedeme alespoň jeden příklad.

 V tabulce 5.2 jsou pro jednotlivé údaje t_i (roky sledovaného období) zaznamenány odpovídající hodnoty y_i(údaje o obratu zahraničního obchodu, uvedené v miliardách peněžních jednotek). Tuto empiricky zjištěnou závislost se pokusíme vyjádřit polynomem k-tého stupně.

Tab. 5.2 Údaje o obratu zahraničního obchodu (v mld. peněžních jednotek)

Při prvním výpočtu je zvolen koeficient determinace r² = 0,85. Pro tento koeficient stanovíme stupeň polynomu k = 1. Příslušnou empiricky zjištěnou závislost lze (při zvoleném r² = 0,85) aproximovat přímkou, přičemž vypočtené hodnoty koeficientů a₀ a a₁ jsou: a₀ = –14,75; a₁= 5,33. Aproximačním polynomem je tedy přímka f(t) = 5,33 t+ 14,75. Je zjevné, že nalezená aproximační funkce neaproximuje danou závislost nejlépe. Proto pro další výpočet stanovíme koeficient determinace r²= 0,95. Výpočtem zjistíme, že stupeň polynomu má hodnotu k = 2 a koeficienty polynomu jsou a₀ = 2,334; a₁ = – 0,699; a₂ = 0,376. Nalezená aproximační funkce má tedy tvar: f(t) = 0,376 t² – 0,699 t + 2,334.

Lze si ověřit (vynesením funkcí do grafů), že tato funkce aproximuje sledovanou empirickou závislost lépe. V dalším výpočtu může stanovit koeficient determinace r²= 0,98 a vypočteme opět tytéž hodnoty koeficientů (a₀= 2,334; a₁ = – 0,699; a₂ = 0,376). Nemá tedy zřejmě smysl měnit dále hodnoty r², aproximační polynom má stále stejné koeficienty (a samozřejmě tedy i stupeň). Vypočtené funkční hodnoty f(t_i) pro jednotlivé t_i (kde i = 1 … 15) pro nalezený polynom f(t) = 0,376 t² – 0,699 t + 2,334 jsou uvedeny v tabulce 5.3.

Na počítači lze vykreslit experimentálně zjištěnou závislost i její aproximaci. Program nám umožňuje vypočíst funkční hodnoty aproximačního polynomu v dalších předem stanovených bodech. Tímto způsobem můžeme prognózovat vývoj empirické závislosti v předem stanoveném časovém intervalu.

Tab. 5.3 Vypočtené funkční hodnoty aproximačního polynomu

Volba vhodné prognostické techniky záleží jenom na jejím účelu a disponibilních údajích. Do značné míry je ovlivňována kvalifikací manažerů, respektive analytiků, kteří prognózy zpracovávají. Těžko lze po někom požadovat, aby pro prognózu využil regresní analýzu, jestliže se s ní dotyčný pracovník dosud neseznámil. Proto také řada organizací nakupuje komplexní dlouhodobé prognózy od různých poradenských firem. I zde je nutné upozornit na to, že nekvalifikovaný manažer může „nakoupenou“ prognózu nesprávně interpretovat a učinit nesprávné rozhodnutí.

^[1]    Logistická funkce je též známá pod názvem Verhulstova-Pearlova funkce, Robertsonova funkce atp.
^[2]    Ter-Manuelianc, A.: Modelování problémů řízení. Institut řízení, Praha 1977.

Převzato z knihy Řízení rizik ve firmách a jiných organizacích vydané nakladatelstvím Grada v roce 2013